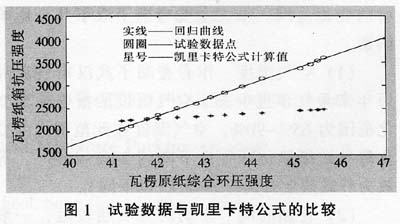
According to the Keli Carter formula, for a specific carton, the linear relationship between the compressive strength of the carton and the integrated ring crush strength of the base paper is consistent with the test results, but the theoretical calculation results of the test data and the Keli Carter formula There is a large error between them (see Figure 1).
Figure 1 shows that the linear relationship between the compressive strength of the test object and the integrated paper crush strength of the base paper is inconsistent with the formula of the Keli Carter. In this paper, a linear regression analysis is performed according to the test data to obtain the linear relationship between the two:
R=338Rx-11849 (3)
Substituting equation (2) into (3) and combining the constants, the formula for calculating the compressive strength of the test carton is:
R=22.24(R1+R2)+32.84Rm-11849 (4)
In reliability analysis, the intensity distribution model of structural materials or components is usually selected as a normal distribution or Weibull distribution model. In this paper, it is assumed that the ring pressure strengths of face paper, inner paper, and core paper are all normally distributed, and their statistical eigenvalues ​​can be calculated from the test data (see Table 1).
3, the calculation of corrugated carton load
Under normal stacking conditions, the bottommost cartons are under the most stress and are most likely to fail due to collapse. In theory, the pressure on the bottommost carton is:
P=W(n-1)×9.81 (5)
In the formula: P-normal stacking under the pressure of the bottom of the carton (N);
Weight of W-carton after loading (kg);
N-stacking number.
Corrugated boxes are inevitably affected by external factors such as conditions of use, storage environment, and placement time. These external factors will cause changes in the compressive strength of the carton. From the point of view of equivalent effects, the compressive strength of the carton The change is completely equivalent to the change in the opposite direction of the external load to which it is subjected, and thus the range of variation of the external load of the corrugated box during the flow can be obtained. This article mainly considers the following factors.
(1) Air humidity The author has reviewed the report on the air humidity in the weather forecast of Wuhan Meteorological Bureau over the years. The change range is 65% to 90%. Changes in the air humidity within this range will result in a reduction in the compressive strength of the carton by approximately 24% to 45%, which is equivalent to an increase in the external load (same as below).
(2) Storage time Milk has a short shelf life, generally 0 to 10 days. The resulting decrease in intensity is about 0-20%.
(3) Stacking mode Normal stacking causes a decrease in strength of about 15 to 20%.
(4) Vibration and Shock of Transportation Tools The vibration and impact of the corrugated carton during transportation will cause the compressive strength to drop by about 20%. However, milk with a short shelf life is generally not transported to a remote place. Therefore, the value of the intensity reduction caused during transport is much smaller than that of general packaged goods. This article considers it to be 0 to 10%.
Assume that the above factors are independent of each other. Their final integrated impact on the load outside the carton can be seen as the product of the effects of all the independent factors under their own influence. From reliability theory, the distribution model of the external load should be a lognormal distribution. It is known that the weight of a single carton is 0.3kg, the weight of milk is 10kg, and the stacking layer number is 15 layers. Based on formula (5) and the above analysis, it can be concluded that the upper and lower limits of the change range of the external load of the carton during circulation are:
The upper limit: (15-1) × 10.3 × 9.81 × (1 + 0.24) × 1 × (1 + 0.15) × 1 = 2017.2 N
The lower limit: (15-1)×10.3×9.81×(1+0.45)×1×(1+0.20)×(1+0.20)×(1+0.10)=3249.1.2 N
The author believes that the load S outside the carton obeys a lognormal distribution, and the probability that its random variation value lies between the upper and lower limits of the variation range calculated in this paper is about 99.74%. The average value of the external load can be calculated from the 3δ rule in probability theory. And standard deviation (see Table 1).
4, corrugated box reliability analysis
4.1 Reliability Calculation
Corrugated box limit state function based on ultimate compressive capability can be expressed as:
g=CrR-CsS (6)
In the formulas, R and S are the ultimate compressive strength of the corrugated box and the external load during the flow; Cr and Cs represent the uncertainty of the analytical model of the compressive strength and external load of the corrugated box.
Substituting equation (4) into (6) yields:
g=Cr [22.24(R1+R2)+32.84Rm-11849]-CsS (7)
This paper assumes that each basic random variable in formula (7) is independent of each other, and their probability distribution models and statistical characteristics are shown in Table 1. JC method was used to calculate the reliability index of corrugated box based on ultimate compressive strength β=0.5166 and reliability pr=0.6973.
4.2 Sensitivity analysis
Table 2 shows the calculation results of the sensitivity factors of each basic random variable. As can be seen from Table 2, the uncertainty of the corrugated cardboard box compressive strength and external load analysis and calculation model is the most important. Followed by the corrugated core paper ring pressure strength and external load, face paper and paper in the ring pressure strength is more.
4.3 Analysis of safety factor
Because the carton compressive strength and external load are random variables. Naturally, the safety factor defined as the ratio of strength to external load is also a random variable. The range of random safety factors is:

Among them, β is the reliability index, CR, CS represent the compressive strength of the carton and the coefficient of variation of the external load, respectively.
From the test data and the calculation results in Table 1, the coefficient of variation of the carton compressive strength and external load can be obtained. Assuming that the coefficient of variation remains unchanged, the range of random safety factor calculated from equation (8) in the case of a reliability pr = 0.99 is: 1 ≤ n ≤ 2.856. In the calculation and calculation of the current compressive strength of corrugated boxes, the safety factor is generally taken as 4 to 5. It can be seen that the current strength design method is somewhat safe. (Wen / Zhou Mingyi Wang Yucheng Pan Yangjin)

Figure 1 shows that the linear relationship between the compressive strength of the test object and the integrated paper crush strength of the base paper is inconsistent with the formula of the Keli Carter. In this paper, a linear regression analysis is performed according to the test data to obtain the linear relationship between the two:
R=338Rx-11849 (3)
Substituting equation (2) into (3) and combining the constants, the formula for calculating the compressive strength of the test carton is:
R=22.24(R1+R2)+32.84Rm-11849 (4)
In reliability analysis, the intensity distribution model of structural materials or components is usually selected as a normal distribution or Weibull distribution model. In this paper, it is assumed that the ring pressure strengths of face paper, inner paper, and core paper are all normally distributed, and their statistical eigenvalues ​​can be calculated from the test data (see Table 1).

3, the calculation of corrugated carton load
Under normal stacking conditions, the bottommost cartons are under the most stress and are most likely to fail due to collapse. In theory, the pressure on the bottommost carton is:
P=W(n-1)×9.81 (5)
In the formula: P-normal stacking under the pressure of the bottom of the carton (N);
Weight of W-carton after loading (kg);
N-stacking number.
Corrugated boxes are inevitably affected by external factors such as conditions of use, storage environment, and placement time. These external factors will cause changes in the compressive strength of the carton. From the point of view of equivalent effects, the compressive strength of the carton The change is completely equivalent to the change in the opposite direction of the external load to which it is subjected, and thus the range of variation of the external load of the corrugated box during the flow can be obtained. This article mainly considers the following factors.
(1) Air humidity The author has reviewed the report on the air humidity in the weather forecast of Wuhan Meteorological Bureau over the years. The change range is 65% to 90%. Changes in the air humidity within this range will result in a reduction in the compressive strength of the carton by approximately 24% to 45%, which is equivalent to an increase in the external load (same as below).
(2) Storage time Milk has a short shelf life, generally 0 to 10 days. The resulting decrease in intensity is about 0-20%.
(3) Stacking mode Normal stacking causes a decrease in strength of about 15 to 20%.
(4) Vibration and Shock of Transportation Tools The vibration and impact of the corrugated carton during transportation will cause the compressive strength to drop by about 20%. However, milk with a short shelf life is generally not transported to a remote place. Therefore, the value of the intensity reduction caused during transport is much smaller than that of general packaged goods. This article considers it to be 0 to 10%.
Assume that the above factors are independent of each other. Their final integrated impact on the load outside the carton can be seen as the product of the effects of all the independent factors under their own influence. From reliability theory, the distribution model of the external load should be a lognormal distribution. It is known that the weight of a single carton is 0.3kg, the weight of milk is 10kg, and the stacking layer number is 15 layers. Based on formula (5) and the above analysis, it can be concluded that the upper and lower limits of the change range of the external load of the carton during circulation are:
The upper limit: (15-1) × 10.3 × 9.81 × (1 + 0.24) × 1 × (1 + 0.15) × 1 = 2017.2 N
The lower limit: (15-1)×10.3×9.81×(1+0.45)×1×(1+0.20)×(1+0.20)×(1+0.10)=3249.1.2 N
The author believes that the load S outside the carton obeys a lognormal distribution, and the probability that its random variation value lies between the upper and lower limits of the variation range calculated in this paper is about 99.74%. The average value of the external load can be calculated from the 3δ rule in probability theory. And standard deviation (see Table 1).
4, corrugated box reliability analysis
4.1 Reliability Calculation
Corrugated box limit state function based on ultimate compressive capability can be expressed as:
g=CrR-CsS (6)
In the formulas, R and S are the ultimate compressive strength of the corrugated box and the external load during the flow; Cr and Cs represent the uncertainty of the analytical model of the compressive strength and external load of the corrugated box.
Substituting equation (4) into (6) yields:
g=Cr [22.24(R1+R2)+32.84Rm-11849]-CsS (7)
This paper assumes that each basic random variable in formula (7) is independent of each other, and their probability distribution models and statistical characteristics are shown in Table 1. JC method was used to calculate the reliability index of corrugated box based on ultimate compressive strength β=0.5166 and reliability pr=0.6973.
4.2 Sensitivity analysis
Table 2 shows the calculation results of the sensitivity factors of each basic random variable. As can be seen from Table 2, the uncertainty of the corrugated cardboard box compressive strength and external load analysis and calculation model is the most important. Followed by the corrugated core paper ring pressure strength and external load, face paper and paper in the ring pressure strength is more.

4.3 Analysis of safety factor
Because the carton compressive strength and external load are random variables. Naturally, the safety factor defined as the ratio of strength to external load is also a random variable. The range of random safety factors is:


Among them, β is the reliability index, CR, CS represent the compressive strength of the carton and the coefficient of variation of the external load, respectively.
From the test data and the calculation results in Table 1, the coefficient of variation of the carton compressive strength and external load can be obtained. Assuming that the coefficient of variation remains unchanged, the range of random safety factor calculated from equation (8) in the case of a reliability pr = 0.99 is: 1 ≤ n ≤ 2.856. In the calculation and calculation of the current compressive strength of corrugated boxes, the safety factor is generally taken as 4 to 5. It can be seen that the current strength design method is somewhat safe. (Wen / Zhou Mingyi Wang Yucheng Pan Yangjin)
A3 Size UV Flatbed Printer,Dx5 UV Flatbed Printer,UV Eco Solvent Printer,UV Flatbed Printer
Hongkong Liyu Technology Co., Ltd. , http://www.chprinterparts.com